Problem: The Super Lotto jackpot is $8 million this week. Should I play?
Strategy: It depends on how many numbers are in the game. You need to figure out the number of possible combinations in the game.
You can use the COMBIN function as follows to figure out the number of possible combinations for games in which you choose 6 of 40, 44, 48, and so on numbers:
- Set up a spreadsheet with the number of balls in the lotto game (40, 44, 48, and so on) in cell A2.
- In cell B2, identify how many numbers you need to select correctly.
- Enter the formula =COMBIN(A2,B2) in cell C2.
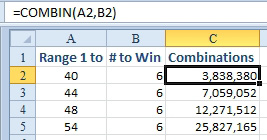
- Combinations of choosing 6 numbers.
If your state lottery game requires you to select 6 numbers out of 40, then the odds against you winning are 3.83 million to 1. For a $1 bet and an $8 million payout, the odds are in your favor.
For a game with 44 numbers, the odds are 7 million to 1. This payoff is only slightly in your favor.
For games with 48 or 54 numbers, the payout is not worth the long odds of the game.
Additional Details: COMBIN figures combinations. Here, the sequence in which the balls are drawn is not relevant. If you had a game in which you had to match both the numbers and the order in which they were drawn, you would want to use the PERMUT function to find the number of permutations of drawing 6 numbers in sequence out of 40.
Additional Details: Since the first edition of this book, two multi-state lotteries have become popular in the United States. These require the player to match five numbers from one pool of numbers and then one number from a separate pool of numbers. This means you have to win two drawings to win the jackpot. Multiply the combinations from the first drawing with the combinations from the second drawing. Here are the calculations for Mega Millions and PowerBall lotteries.
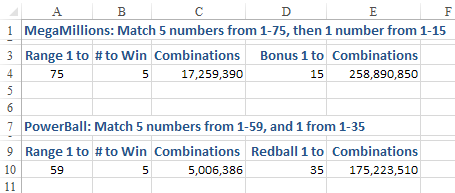
- The odds are much higher for these lotteries.
It only makes statistical sense to play the $1 Mega Millions when the jackpot is above $259 million. Because the PowerBall costs $2 to play, it only makes sense when the jackpot is above $350 million. As you can see, lotteries are a tax on people who can't use Excel.

