Problem: I work for a quickly growing company. In the first year, we had $970,000 in sales. In the fifth year, we had $6,175,000 in sales. I need to determine our compounded annual growth rate.
Strategy: Sales in the fifth year are 6,175/970 higher than in the first year. The formula for growth is (Year5/Year1) - 100% or 537%.
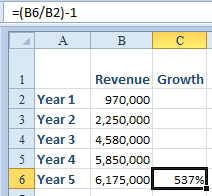
- Five-year growth rate.
However, a compounded growth rate is a number, x, that will calculate like this:
Year1 * (100% + x) * (100% + x) * (100% + x) * (100% + x) = Year5
This is the same as: Year1 * (100% + x)^4 = Year5
So, in order to calculate x, you have to be able to find the fourth root of (Year5/Year1). The formula to find the fourth root is to raise the number to the 1/4 power. Thus, the formula to calculate the compounded growth rate is: (Year5/Year1)^(1/4)-100% = x.
To prove that this formula is working, multiply year 1 by 1.5884235 four times. The answer should be very close to Year 5.
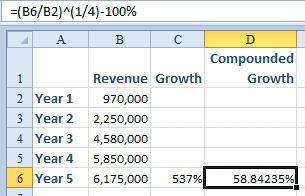
- Compounded growth rate.
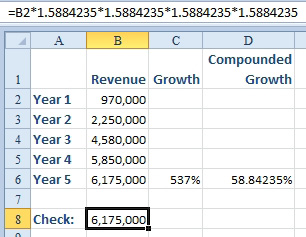
- Prove that the 58.84% growth rate is accurate.

